Question

What is the solution to the equation m/m+4+4/4-m=m^2/m^2-16

Answer 1

B) -2

Explanation:

Answer 2

The solution is m = -2

Explanation:

The given rational equation is

`(m)/(m+4)+(4)/(4-m)=(m^2)/(m^2-16)`

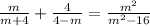
We'll simplify the left hand side first.

The LCD is (m+4)(4-m)

Hence, multiply and divide the first term by 4-m and second by m +4

`(m(4-m))/((m+4)(4-m))+(4(m+4))/((4-m)(m+4)=(m^2)/(m^2-16)`

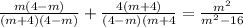
Use the difference of squares rule
`a^2-b^2=(a+b)(a-b)`

`(m(4-m))/(4^2-m^2)+(4(m+4))/(4^2-m^2)=(m^2)/(m^2-16)`

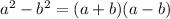
We can now add the numerator

`(m(4-m)+4(m+4))/(4^2-m^2)=(m^2)/(m^2-16)`

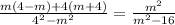
On simplifying, we get

`(4m-m^2+4m+16)/(16-m^2)=(m^2)/(m^2-16)`

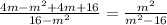
Add the like terms

`(8m-m^2+16)/(16-m^2)=(m^2)/(m^2-16)`

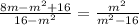
Multiply and divide left hand side by -1

`(m^2-8m-16)/(m^2-16)=(m^2)/(m^2-16)`

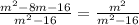
We can cancel the denominator

`-8m-16=0\\8m=-16`

Divide both sides by 8

`m=-2`

The solution is m = -2