Question

Pottery shards were recovered from an archeological dig, as shown in the figure above. Based upon the large edge piece, it is possible to use properties of chords to determine the diameter of the plate. Calculate the diameter of the plate.

Answer 1

Given:

AB=BC=5 inches, and BD=2.5 inches.

BD is the perbenticular bisector of AC.

Required:

We need to find the diameter of the given plate.

Step-by-step explanation:

Let O be the center of the circle.

The radius of the circle, AO=r.

DO also the radius of the circle, DO=r.

`DO=BD+BO`

Substitute DO=r and BD=2.5 inches in the equation.

`r=2.5+BO`
`BO=r-2.5`

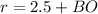
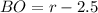
Consider the right angle triangle ABO.

Use the Pythagorean theorem.

`AO^2=AB^2+BO^2`

Substitute AO=r, AB=5, and BO=r-2.5 in the equation.

`r^2=5^2+(r-2.5)^2`
`Use\text{ }(a-b)^2=a^2-2ab+b^2.\text{ Here a=r and b =2.5.}`

`r^2=5^2+r^2-2*2.5r+(2.5)^2`

`r^2=25+r^2-5r+6.25`

`r^2=r^2-5r+31.25`

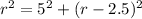
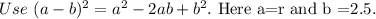
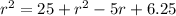
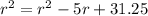
Solve for r.

`5r=31.25`

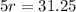
Divide both sides by 5.

`(5r)/(5)=(31.25)/(5)`
`r=6.25`

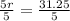
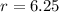
We ge radius, r =6.25.

`\text{We know that the diameter =2}* radius.`

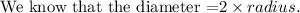
Substitute radius = 6.25 in the equation.

`Diameter=2*6.25`

`Diameter=12.5\text{ inches.}`

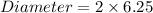
Final answer:

`Diameter=12.5\text{ inches.}`