Question

Take another guess: A student takes a multiple-choice test that has 8 questions. Each question has four choices. The student guesses randomly at each answer. Round the answers to three decimal places.(a) Find P(3)P(3) =(b) Find P (More than 1).P(More than 1)=

Answer 1

(a)0.208

(b)0.633

Step-by-step explanation:

Since the variable X is not defined, we assume that X is the number of questions answered correctly.

Each question has 4 options out of which just 1 is correct.

Each question is independent of other questions. Thus, we can use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`\begin{gathered} P(X=x)=^nC_x(p^x)(1-p)^(n-x) \\ where\; ^nC_x=(n!)/((n-x)!x!) \end{gathered}`

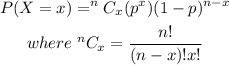
• In this case, there are 8 questions: n=8

,

• 1 out of 4 options is correct, p=1/4=0.25

Part 1

`\begin{gathered} P(3)=^8C_3(0.25^3)(1-0.25)^(8-3) \\ =56*0.25^3*0.75^5 \\ =0.208 \end{gathered}`

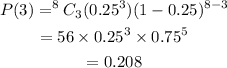
P(3)=0.208 correct to 3 decimal places.

Part 2

`P(X>1)=1-P(X\le1)`

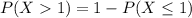
First, we calculate P(X≤1):

`\begin{gathered} P\mleft(X\le1\mright)=P(0)+P(1) \\ P(0)=^8C_0(0.25^0)(0.75)^8=1*1*0.1001=0.1001 \\ P(1)=^8C_1(0.25^1)(0.75)^7=8*0.25*0.1335=0.2670 \\ \implies P(X\le1)=0.1001+0.2670=0.3671 \end{gathered}`

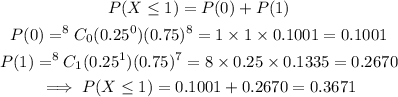
Therefore, the probability, P(more than 1) is:

`P(X>1)=1-P(X\le1)=1-0.3671=0.633`

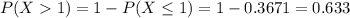
P(more than 1) is 0.633 (correct to 3 decimal places).