Question

Consider the complex number z = 1+iV3.Which of the following complex numbers best approximates z4?Hint: z has a modulus of 2 and an argument of 60”.Choose 1 answer:А4- 6.9iB-4 - 6.918 – 13.97–8 – 13.94

Answer 1

A complex number z with modulus |z| and argument θ can be written as:

`z=|z|\cdot(\cos \theta+i\sin \theta)`

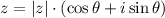
And the nth power of z can be written as:

`z^n=|z|^n\cdot\lbrack\cos (n\theta)+i\sin (n\theta)\rbrack`

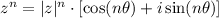
Thus, using the given hint, we have:

`\begin{gathered} |z|=2 \\ \theta=60^(\circ) \end{gathered}`

So, the fourth power of z is given by:

`\begin{gathered} z^4=2^4\cdot\lbrack\cos (4\cdot60^(\circ))+i\sin (4\cdot60^(\circ))\rbrack \\ \\ z^4=16\cdot\lbrack\cos (240^(\circ))+i\sin (240^(\circ))\rbrack \end{gathered}`

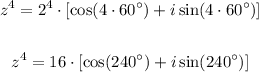
Now, notice that:

`\begin{gathered} \cos (240^(\circ))=-(1)/(2) \\ \\ \sin (240^(\circ))=-\frac{\sqrt[]{3}}{2} \end{gathered}`

So, we obtain:

`z^4=16\mleft(-(1)/(2)-\frac{\sqrt[]{3}}{2}i\mright)=-(16)/(2)-(16)/(2)\sqrt[]{3}i=-8-8\sqrt[]{3}i\cong-8-13.9i`

Therefore, option D is correct.