Answer:
a. The common ratio is 0.5
b) The value of the first term is 29
c) The sum of the first 5 terms is 56.1875
Explanation:
The nth term of the geometric sequence is a
 = a
= a
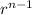 , where
, where
The sum of the nth term is S
 =
=
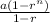
∵ The second term of a geometric sequence is 14.5
∴ n = 2
∴ a
 = 14.5
= 14.5
∵ a
 = ar
= ar
→ Equate the right sides of a
 by 14.5
by 14.5
∵ ar = 14.5 ⇒ (1)
∵ The fifth term is 1.8125
∴ n = 5
∴ a
 = 1.8125
= 1.8125
∵ a
 = a
= a
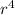
→ Equate the right sides of a
 by 14.5
by 14.5
∵ a
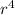 = 1.8125 ⇒ (2)
= 1.8125 ⇒ (2)
→ Divide equation (2) by equation (1)
∵
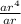 =
=
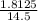
∴ r³ = 0.125
→ Take ∛ for both sides
∴ r = 0.5
a. The common ratio is 0.5
→ Substitute the value of r in equation (1) to find a
∵ a(0.5) = 14.5
∴ 0.5a = 14.5
→ Divide both sides by 0.5
∴ a = 29
b) The value of the first term is 29
∵ n = 5
∴ S
 =
=
![(29[1-[0.5]^(5)))/(1-0.5)](https://img.qammunity.org/2022/formulas/mathematics/high-school/at6zmw50he0ub6274ngjtroyzebp8q8xul.png)
∴ S
 = 56.1875
= 56.1875
c) The sum of the first 5 terms is 56.1875