Answers:
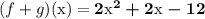
Domain = set of all real numbers
========================================================
Work Shown:

The domain of each f(x) and g(x) is "set of all real numbers" since we can replace x with any real number to get some output.
By extension, this means the domain of (f+g)(x) is also "set of all real numbers".
It turns out any polynomial will have this domain. We don't have to worry about things like applying square roots to negatives, or dividing by zero. This is why there isn't a restriction on x.
To write "set of all real numbers" in interval notation, we would say
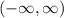 to indicate x is anything between negative infinity and positive infinity.
to indicate x is anything between negative infinity and positive infinity.