Question

A parabola is given by the equation y2 = -24x. The equation of the directrix of the parabola is

Answer 1

Explanation:

Answer 2

`x=6`

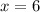
Explanation:

We have been given an equation of a parabola
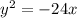`y^2=-24x`. We are asked to find the equation of directrix of the given parabola.

First of all, we will convert our given equation in standard form of right-left opening parabola:
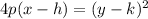`4p(x-h)=(y-k)^2`, where,
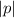`|p|` represents focal length and (h,k) is vertex of parabola.

We can rewrite our given equation as:

`-24x=y^2`

`4(-6)(x-0)=(y-0)^2`

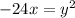
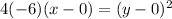
Since our given parabola has a
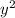`y^2` term, so it will be symmetric about x-axis.

The vertex of parabola is (0,0) and focal length is 6.

We know that equation of directrix of right-left opening parabola is
`x=h-p`.

`x=0-(-6)`

`x=0+6`

`x=6`

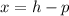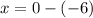
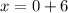
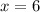
Therefore, the equation of the directrix of our given parabola is
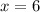`x=6`.