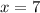Question

Figure ABCD is a parallelogram.
What is the value of x?

Answer 1

`x=7`

Explanation:

We have been given a parallelogram. We are asked to find the value of x for the given parallelogram.

We know that opposite sides of parallelogram are equal in measure, so side AD will be equal to BC.

We can represent this information in an equation as:

`AD=BC`

`5x+3=38`

Subtract 3 from both sides:

`5x+3-3=38-3`

`5x=35`

Divide both sides by 5:

`(5x)/(5)=(35)/(5)`

`x=7`

Therefore, the value of x is 7.

Answer 2

For this case the first thing you should do is look at the sides that are parallel.

We have then that the AD side is parallel to the BC side.

Therefore, it is true that:

`AD = BC`

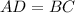
Therefore, substituting values we have:

`5x + 3 = 38`

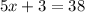
From here, we clear the value of x.

We have then:

`5x = 38-3`

`5x = 35`

`x = (35)/(5)`

`x = 7`

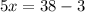
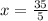
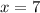
Answer:

The value of x is equal to 7.

`x = 7`