Question

A 255 g sample of ice at 0.0 0C was melted and its temperature increased to 22 0C. What was the amount of heat (q) transferred?

Heat of fusion for water (ΔHfus) is 334 j/g
The specific heat of water is 4.18 J/g • 0C
This is a two step process. What steps are necessary to solve the problem?

Answer 1

`\Delta H_T=108,620J=108.6kJ`

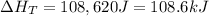
Step-by-step explanation:

Hello!

In this case, since we can evidence that the ice is firstly undergoing a melting process at constant 0.0 °C, whose associated enthalpy change is:

`\Delta H_1 =m\Delta H_(fus)`

Next, the formed liquid water undergoes a heating from 0.0 °C to 22°C, to the associated enthalpy change is:

`\Delta H_2 =mC_(liq)(22\°C-0.0\°C)`

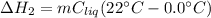
Thus, the total enthalpy change, or heat added to the system turns out:

`\Delta H_1 =255g*334(J)/(g)=85,170J\\\\ \Delta H_2=255g*4.18(J)/(g\°C)*(22\°C-0.0\°C)=23,449.8J\\\\ \Delta H_T=85,170J+23,449.8J\\\\\Delta H_T=108,620J=108.6kJ`

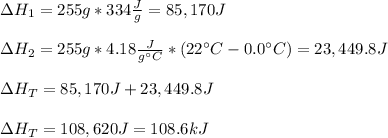
Best regards!