Answer: Third option is correct.
Explanation:
since we have given that
Length of first string = 43 cm
Angle of elevation with the horizontal = 50°
Length of second string = 35 cm
Angle of elevation with the horizontal = 70°
We need to find the distance between the points of suspension of the strings on the ceiling .
WE will use "Cosine Law".
In ΔABC,
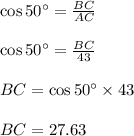
Similarly,
In ΔPCR,
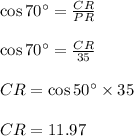
So, Total distance between the points of suspension of the strings on the ceiling is given by
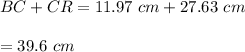
Hence, third option is correct.