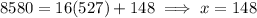Question

Find an integer x such that 0<=x<527 and x^37===3 mod 527

Answer 1

Since
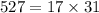
`527=17*31`, we have that


`x^(37)\equiv3\mod{527}\implies\begin{cases}x^(37)\equiv3\mod{17}\\x^(37)\equiv3\mod{31}\end{cases}`

By Fermat's little theorem, and the fact that
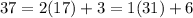
`37=2(17)+3=1(31)+6`, we know that


`x^(37)\equiv(x^2)^(17)x^3\equiv x^5\mod{17}`

`x^(37)\equiv(x^1)^(31)x^6\equiv x^7\mod{31}`

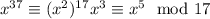
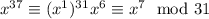
so we have


`\begin{cases}x^5\equiv3\mod{17}\\x^7\equiv3\mod{31}\end{cases}`

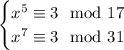
Consider the first case. By Fermat's little theorem, we know that


`x^(17)\equiv x^(16)x\equiv x\mod{17}`

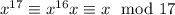
so if we were to raise
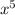
`x^5` to the
`n`th power such that


`(x^5)^n\equiv x^(5n)\equiv x\mod{17}`

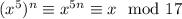
we would need to choose
`n` such that
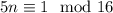
`5n\equiv1\mod{16}` (because
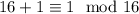
`16+1\equiv1\mod{16}`). We can find such an
`n` by applying the Euclidean algorithm:


`16=3(5)+1`

`\implies1=16-3(5)`

`\implies16-3(5)\equiv-3(5)\equiv1\mod{16}`

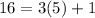
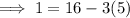
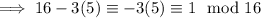
which makes
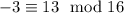
`-3\equiv13\mod{16}` the inverse of 5 modulo 16, and so
`n=13`.

Now,


`x^5\equiv3\mod{17}`

`\implies (x^5)^(13)\equiv x^(65)\equiv x\equiv3^(13)\equiv(3^4)^2*3^4*3^1\mod{17}`


`3^1\equiv3\mod{17}`

`3^4\equiv81\equiv4(17)+13\equiv13\equiv-4\mod{17}`

`3^8\equiv(3^4)^2\equiv(-4)^2\mod{17}`

`\implies3^(13)\equiv(-4)^2*(-4)*3\equiv(-1)*(-4)*3\equiv12\mod{17}`

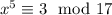
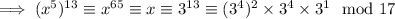
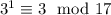
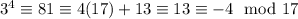
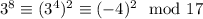
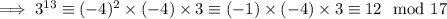
Similarly, we can look for
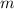
`m` such that
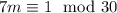
`7m\equiv1\mod{30}`. Apply the Euclidean algorithm:


`30=4(7)+2`

`7=3(2)+1`

`\implies1=7-3(2)=7-3(30-4(7))=13(7)-3(30)`

`\implies13(7)-3(30)\equiv13(7)equiv1\mod{30}`

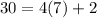
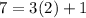
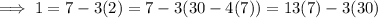
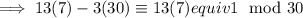
so that
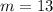
`m=13` is also the inverse of 7 modulo 30.

And similarly,


`image`

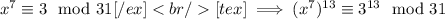
Decomposing the power of 3 in a similar fashion, we have


`3^(13)\equiv(3^3)^4*3\mod{31}`


`3\equiv3\mod{31}`

`3^3\equiv27\equiv-4\mod{31}`

`\implies3^(13)\equiv(-4)^4*3\equiv256*3\equiv(8(31)+8)*3\equiv24\mod{31}`

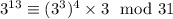
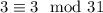
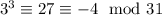
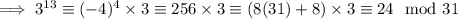
So we have two linear congruences,


`\begin{cases}x\equiv12\mod{17}\\x\equiv24\mod{31}\end{cases}`

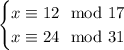
and because
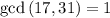
`\mathrm{gcd}\,(17,31)=1`, we can use the Chinese remainder theorem to solve for
`x`.

Suppose
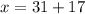
`x=31+17`. Then modulo 17, we have


`x\equiv31\equiv14\mod{17}`

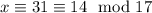
but we want to obtain
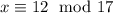
`x\equiv12\mod{17}`. So let's assume
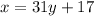
`x=31y+17`, so that modulo 17 this reduces to


`x\equiv31y+17\equiv14y\equiv1\mod{17}`

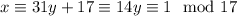
Using the Euclidean algorithm:


`17=1(14)+3`

`14=4(3)+2`

`3=1(2)+1`

`\implies1=3-2=5(3)-14=5(17)-6(14)`

`\implies-6(14)\equiv11(14)\equiv1\mod{17}`

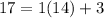
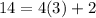
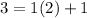
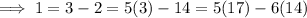
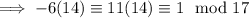
we find that
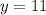
`y=11` is the inverse of 14 modulo 17, and so multiplying by 12, we guarantee that we are left with 12 modulo 17:


`x\equiv31(11)(12)+17\equiv12\mod{17}`

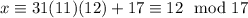
To satisfy the second condition that
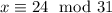
`x\equiv24\mod{31}`, taking
`x` modulo 31 gives


`x\equiv31(11)(12)+17\equiv17\mod{31}`

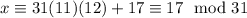
To get this remainder to be 24, we first multiply by the inverse of 17 modulo 31, then multiply by 24. So let's find
`z` such that
`17z\equiv1\mod{31}`. Euclidean algorithm:


`31=1(17)+14`

`17=1(14)+3`

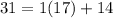
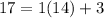
and so on - we've already done this. So
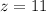
`z=11` is the inverse of 17 modulo 31. Now, we take


`x\equiv31(11)(12)+17(11)(24)\equiv24\mod{31}`

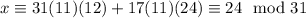
as required. This means the congruence
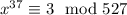
`x^(37)\equiv3\mod{527}` is satisfied by


`x=31(11)(12)+17(11)(24)=8580`

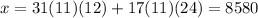
We want
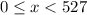
`0\le x<527`, so just subtract as many multples of 527 from 8580 until this occurs.


`8580=16(527)+148\implies x=148`