Question

From a boat on the lake, the angle of elevation to the top of a cliff is 26°35'. If the base of the cliff is 85 feet from the boat, how high is the cliff (to the nearest foot)?

Answer 1

check the picture below

now, 26°35' is just 26bdegrees and 35 minutes

your calculator most likely will have a button [ ° ' " ] to enter degrees and minutes and seconds

there are 60 minutes in 1 degree and 60 seconds in 1 minute

so.. you could also just convert the 35' to 35/60 degrees

so
`\bf 26^o35'\implies 26+(35)/(60)\implies \cfrac{1595}{60}\iff \cfrac{319}{12} \\\\\\ tan(26^o35')\iff tan\left[ \left( \cfrac{391}{12} \right)^o \right]`

now, the angle is in degrees, thus, make sure your calculator is in Degree mode

Answer 2

`x=42.5 feet`

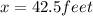
Explanation:

It is given that From a boat on the lake, the angle of elevation to the top of a cliff is 26°35'. If the base of the cliff is 85 feet from the boat, thus using trigonometry, we have

`(AB)/(AC)=tan26^(\circ)35'`

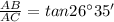
Substituting the given values, we get

`(x)/(85)=tan26.6^(\circ)`

⇒
`x=85(tan26.6^(\circ))`

⇒
`x=85(0.500)`

⇒
`x=42.5 feet`

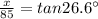
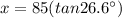
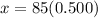
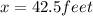
Therefore, the height of the cliff is 42.5 feet.