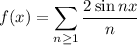Question

Find the half range Fourier sine series of the function

f(x)=π-x -π

Answer 1

The full range is
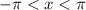
`-\pi<x<\pi` (length
`2L=2\pi`), so the half range is
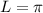
`L=\pi`. The half range sine series would then be given by


`f(x)=\displaystyle\sum_(n\ge1)b_n\sin\frac{n\pi x}L=\sum_(n\ge1)b_n\sin nx`

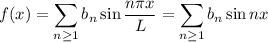
where


`b_n=\displaystyle\frac2L\int_0^Lf(x)\sin\frac{n\pi x}L\,\mathrm dx=\frac2\pi\int_0^\pi(\pi-x)\sin nx\,\mathrm dx`

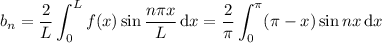
Essentially, this is the same as finding the Fourier series for the function


`\begin{cases}g(x)=\begin{cases}\pi-x&\text{for }0<x<\pi\\-\pi-x&\text{for }-\pi<x<0\end{cases}\\g(x+2\pi)=g(x)\end{cases}`

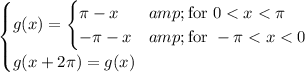
Integrating by parts yields


`b_n=\frac2\pi\left(\frac\pi n-(\sin n\pi)/(n^2)\right)=\frac2n`

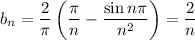
So the half range sine series for this function is simply


`f(x)=\displaystyle\sum_(n\ge1)\frac{2\sin nx}n`