Question

The line y=x+k is a tangent of the circle (x-2)^2+y^2=9, find the possible value/s of k

I need a definite answer not in terms of x or y.
Also I want to know how you arrived at the answer.

Answer 1

`k=-2 +3√(2), \quad k=-2 -3√(2)`

Explanation:

Given equation of the circle:

`(x-2)^2+y^2=9`

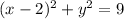
The tangent of a circle is a straight line that touches a circle at one point.

If the line y = x + k is a tangent of the given circle, it will intersect the circle.

Therefore, substitute the equation of the tangent line into the equation of the circle:

`\implies (x-2)^2+(x+k)^2=9`

`\implies x^2-4x+4+x^2+2kx+k^2=9`

`\implies x^2-4x+4+x^2+2kx+k^2-9=0`

`\implies 2x^2+(2k-4)x+(k^2-5)=0`

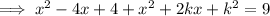
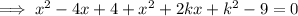
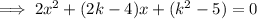
Two lines with the same slope (but different y-intercepts) can be the tangents to the circle at two different points, so there are two possible values of k.

To find k, use the discriminant and set it to zero (if the discriminant equals zero there are two solutions).

Discriminant

`\boxed{b^2-4ac}\quad\textsf{when}\:ax^2+bx+c=0`

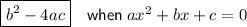
Therefore:

`a=2, \quad b=(2k-4), \quad c=(k^2-5)`

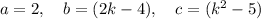
Substitute the values into the discriminant formula:

`\implies b^2-4ac=0`

`\implies (2k-4)^2-4(2)(k^2-5)=0`

`\implies 4k^2-16k+16-8k^2+40=0`

`\implies -4k^2-16k+56=0`

`\implies -4(k^2+4k-14)=0`

`\implies k^2+4k-14=0`

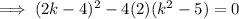
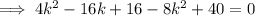
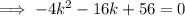
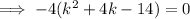
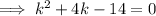
Use the quadratic formula to solve the quadratic.

`\boxed{x=(-b \pm √(b^2-4ac))/(2a)}\quad\textsf{when }\:ax^2+bx+c=0`

`\implies k=(-4 \pm √(4^2-4(1)(-14)))/(2(1))`

`\implies k=(-4 \pm √(16+56))/(2)`

`\implies k=(-4 \pm √(72))/(2)`

`\implies k=(-4 \pm √(36 \cdot 2))/(2)`

`\implies k=(-4 \pm √(36) √(2))/(2)`

`\implies k=(-4 \pm 6 √(2))/(2)`

`\implies k=-2 \pm 3√(2)`

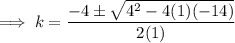
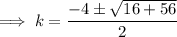
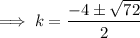
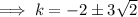
Therefore, the possible values of k are:

`k=-2 +3√(2), \quad k=-2 -3√(2)`