Question

Using the quadratic formula to solve x2 = 5 – x, what are the values of x?

Answer 1

hello :
the discriminat of each quadratic equation : ax²+bx+c=0 ....(a ≠ 0) is :
Δ = b² -4ac
1 ) Δ > 0 the equation has two reals solutions : x = (-b±√Δ)/2a
2 ) Δ = 0 : one solution : x = -b/2a
3 ) Δ < 0 : no reals solutions
in this exercice : x² = 5-x
x² +x-5 = 0 .... a =1 b= 1 c=-5
calculate Δ..................................

Answer 2

`x_(1)=(-1б 4.58)/(2) = 3.58\\\\x_(2)=(-1б -4.58)/(2) =-5.58`

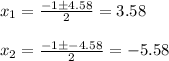
Explanation:

Hello

In elementary algebra, the quadratic formula is the solution of the quadratic equation.

let a polynom

`ax^(2) +bx+c=0`

this can be solved d by using the quadratic equation formula

`x= \frac{-bб \sqrt{b^(2)-4ac } }{2a}`

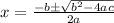
Let

`x^(2) =5-x`

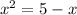
Step 1

do the equation=0

`x^(2) =5-x\\x^(2)+x-5=0`

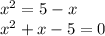
define

`a=1\\b=1\\c=-5\\`

Sep two

put the values into the equation

`x= \frac{-bб \sqrt{b^(2)-4ac } }{2a}\\\\\\x= \frac{-(1)б \sqrt{(1)^(2)-4(1)(-5) } }{2*1}\\x= (-1б √(1+20 ) )/(2)\\x= (-1б 4.58)/(2)\\\\x_(1)=(-1б 4.58)/(2) = 3.58\\\\x_(2)=(-1б -4.58)/(2) =-5.58\\\\`

Have a good day.