Answer:
The midpoints of the EF is (2a,a) .
Explanation:
Definition of midpoints.
The midpoint is the point lie in middle of a line segment. It is equidistant from both endpoints .
Formula
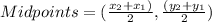
Quadrilateral EFGH has coordinates E(a, a), F(3a, a), G(2a, 0), and H(0, 0).
Now find out the midpoints of the E(a, a) and F(3a, a) .
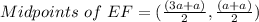
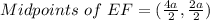
Midpoints of EF = (2a,a)
Therefore the midpoints of the EF is (2a,a) .