Question

In the pendulum formula , we use g = 9.8 m/s2 for the acceleration due to gravity on Earth. But what about on Mars? If an astronaut on the surface of Mars swings a 1-meter long pendulum, and it has a period of 3.27 seconds, what is the acceleration due to gravity, g, on Mars?

Answer 1

Acceleration would be 3.7 m/s² due to gravity on Mars.

Explanation:

We use the pendulum formula :

T =
`2\pi \sqrt{(L)/(g) }`

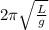
Where L = 1 n

T = 3.27 seconds

∴ 3.27 =
`2\pi \sqrt{(1)/(g) }`

=
`(3.27)/(2\pi ) =\sqrt{(1)/(g) }`

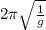
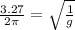
= 0.5207 =
`\sqrt{(1)/(g) }`

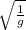
= 0.2711 =
`(1)/(g)`

= g =
`(1)/(0.2711)`

g = 3.68 m/s² or 3.7 m/s²

Acceleration would be 3.7 m/s² due to gravity on Mars.