Question

show the table, intercepts, domain and range, positive and negative intervals, and increasing and decreasing intervals for f(x)=-3x²+1. also table only has to be x values of -3,-2,-1,0,1,2,3

Answer 1

By positive and negative intervals it means that we want the intervals for which the function takes positive/negative values (that is, the graph is above/under the x-axis). Consider the following drawing as an example:

In this case, our function takes positive values on the interval [0,1] and [3,4] and it takes negative values on the interval [1,3] .

In this case, consider the function f(x) = -3x^2+1. If we plot the graph of this function, we get the following

Recall that the intervals are defined for the values of the x axis. In the following picture I will draw the intervals (red-positive, blue-negative)

In this case, the positive interval would be between the x-intercept. So far, we don't where the x-intercept is, but lets say that the graph crosses at points -a and a. Then, in this case the positive interval would be [-a,a]. In case of the negative interval, we will have the intervals (-infinity,-a) and the interval (a, infinity)

By making -3x^2+1 =0 we would find that

`x^2\text{ = }\frac{\text{ -1}}{\text{ - 3}}=\text{ }(1)/(3)`

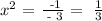
So x = 0.577 or x=-0.577. So a = 0.577

ok, now, we should find the intervals for which the function increases or decreases. We can also determine this with the graph. Increasing means that if x increases (that is, you move to the right in the x-axis), then the value of the function if greater than before (that is, the graph moves up). For decreasing, the idea is the same, but the value of the function decreases as x increases. So, if we draw the increasing(red) and decreasing interval we get

which corresponds to the interval (-infinity, 0) for increasing and (0,infinity) for decreasing.