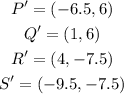Answer:
The coordinates of P',Q',R',S' are;
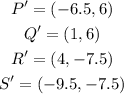
Step-by-step explanation:
Given the quadrilateral PQRS as shown on the diagram.
To determine the coordinates of the figure P'Q'R'S' which is the dilated image of PQRS. Let us apply the formula below;
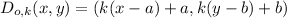
Where;
the center of dilation is (a,b)
the scale factor is k
Given;
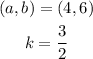
And from the image PQRS;
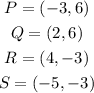
We can then calculate the coordinates of their respective P',Q',R' and S' using the formula;
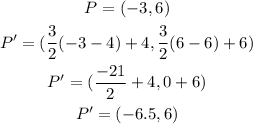
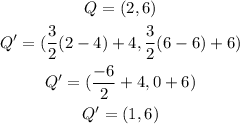
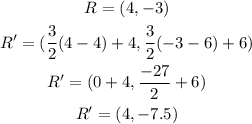
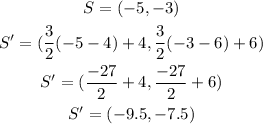
Therefore, the coordinates of P',Q',R',S' are;