Question

EO LINEAR EQUATIONSSolving a word problem with three unknowns using a linear...Over the last three evenings, Keisha received a total of 90 phone calls at the call center. The third evening, she received 3 times as many calls as the secondevening. The first evening, she received 10 fewer calls than the second evening. How many phone calls did she receive each evening?

Answer 1

Given:

a.) Over the last three evenings, Keisha received a total of 90 phone calls at the call center.

b.) The third evening, she received 3 times as many calls as the second evening.

c.) The first evening, she received 10 fewer calls than the second evening.

Let's first express the given relationships into an equation.

Let,

x = number of calls on the 1st evening

y = number of calls on the 2nd evening

z = number of calls on the 3rd evening

Over the last three evenings, Keisha received a total of 90 phone calls at the call center.

`\text{ x + y + z = 90}`

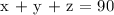
The third evening, she received 3 times as many calls as the second evening.

`\text{ z = 3y}`

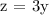
The first evening, she received 10 fewer calls than the second evening.

`\text{ x = y - 10}`

Let's substitute z = 3y and x = y - 10 in x + y + z = 90 to find y.

`\text{ x + y + z = 90}`
`\text{ (y - 10) + y + (3y) = 90}`
`\text{ y - 10 + y + 3y = 90}`
`\text{ y + y + 3y = 90 + 10}`
`\text{5y = 1}00\text{ }\rightarrow\text{ }\frac{\text{5y}}{5}\text{ = }\frac{\text{1}00}{5}`
`\text{ y = 20 calls}`

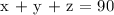
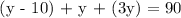
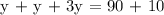
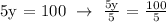
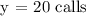
Therefore, there are 20 calls on the 2nd evening.

Let's now determine how many calls are there on the 1st and 3rd evenings.

y = 20

z = 3y

= 3(20)

z = 60

x = y - 10

= 20 - 10

x = 10

In summary:

There are 10 calls on the 1st evening.

There are 20 calls on the 2nd evening.

Therefore 60 calls on the 3rd evening.