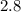Question

Graph the line y= x+1. What point on the line is the short distance from the point (4,1)? What is the distance? Round to the nearest tenth.

Answer 1

To graph a line we have to obtain two points on the line.

If we evaluate the given equation at x=0, we get:

`y=1,`

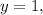
therefore, the point (0,1) is on the line.

Now, if we set y=0, and solve for x we get:

`x=-1,`

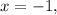
therefore, point (-1,0) is on the line.

With the two points we found, we construct the line that passes through those points.

The graph of the line is:

Now, recall that the shortest distance from a point to a line is the length of a perpendicular line from the point to the line.

Recall that a perpendicular line to a given line has slope -1/m where m is the slope of the line. Therefore, the line that is perpendicular to the given line has slope -1 and passes through the point (4,1), (using the slope-point formula for the equation of the line) has equation:

`y-1=-1(x-4)\text{.}`

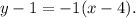
The graph of the two lines and the point is:

From the above graph, we get that the distance from (4,1) to the line is the distance between points (4,1) and (2,3). Using the formula for the distance between two points we get:

`d=\sqrt[]{(4-2)^2+(1-3)^2}=\sqrt[]{4+4}=\sqrt[]{8}=2\sqrt[]{2}.`

Answer:

Graph: (using the points (0,1) and (-1,0))

Distance:

`2.8`