Question

Two ships 1/4 miles apart estimate ocean depth. To do this, ship A sends a sonar beam at 85 degrees to the surface. Ship B receives the beam at 87 degrees after it is reflected off the bottom. What is the oceans depth under ship A?

Answer 1

To answer this question, let us make a diagram for proper illustration

From the diagram above, two alternate angles of 5 degrees and 3 degrees will add up to give us 8 degrees. So the angle facing the side 0.25 miles is 8 degrees

Note that 0.25 miles was gotten thus

`(1)/(4)=0.25\text{ miles }`

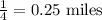
Now, extracting the triangle we need, we have

Now we will find x, using figure a, and then y using the second triangle.

From the first triangle, to find x, we will use the sine rule. From the sine rule,

`\begin{gathered} (x)/(\sin87^o)=(0.25)/(\sin8^o) \\ x=(\sin87^o*0.25)/(\sin8^o) \\ x=1.79386\text{ } \end{gathered}`

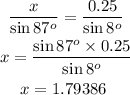
But the ocean depth under ship A is represented as y in our diagram. So we have to find y. Using the trig-ratio

`\begin{gathered} \cos ^{}\theta=\frac{adjacent}{\text{hypotenuse}} \\ \cos 5^o=(y)/(x) \\ y=x\cos 5^o \\ y=1.79386*\cos 5^o \\ y=1.787036 \\ y=1.787\text{ miles } \end{gathered}`

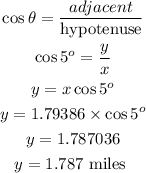
Hence, the answer is 1.787 miles to 3 decimal places