hello
to solve this question we would first of all find the slope of the line

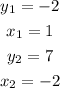
we can now substitute this into the equation

the slope of the line is -3
we can write out how the equation looks
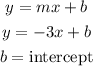
we can use one of the points to solve for b
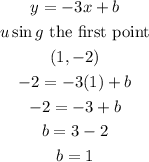
we can now rewrite our equation with slope and intercept
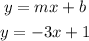
from the calculation above, the equation of the line is given as y = -3x + 1