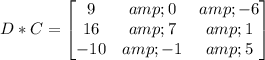Question

Answer the following question No it is not a greater quiz or test just practice

Answer 1

With the given matrices, we need to solve the next operations:

A*B =

`\begin{gathered} A=\begin{bmatrix}{5} & {-1} & {\placeholder{⬚}} \\ {4} & -{2} & {\placeholder{⬚}} \\ {-3} & {6} & {\placeholder{⬚}}\end{bmatrix} \\ B=\begin{bmatrix}{1} & {-3} \\ {2} & {5}\end{bmatrix} \end{gathered}`

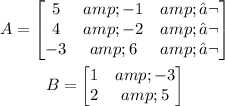
To multiply two matrices, A needs to have the same number of columns as the number of rows for B.

Then, A is a matrix 3x2

B is a matrix 2x2

Now, we need to multiply columns by rows:

`A\ast B=\begin{bmatrix}{(5\ast1)+(-1\ast2)} & {(5\ast-3)+(-1\ast5)} & {\placeholder{⬚}} \\ {(4\ast1)+(-2\ast2)} & {(4\ast-3)+(-2\ast5)} & {\placeholder{⬚}} \\ (-3\ast1)+(6\ast2){} & {(-3\ast-3)+(6\ast5)} & {\placeholder{⬚}}\end{bmatrix}`

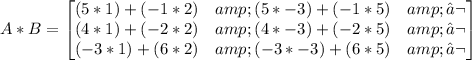
Simplify

`A\ast B=\begin{bmatrix}{3} & {-20} & {\placeholder{⬚}} \\ {0} & {-22} & {\placeholder{⬚}} \\ {9} & {39} & {\placeholder{⬚}}\end{bmatrix}`

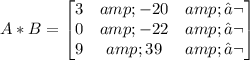
Now, let us find 2B + C

First, let us find 2B:

`2B=2\begin{bmatrix}{1} & {-3} \\ {2} & {5}\end{bmatrix}=\begin{bmatrix}{2} & {-6} \\ {4} & {10}\end{bmatrix}`

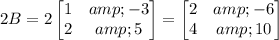
Now, we need to find 2B + C. However, to add up to two matrices they must have the same number of rows and columns.

Therefore, it is not possible to do 2B + C.

3A- D =

Let us find 3A

`3A=3\begin{bmatrix}{5} & {-1} & {\placeholder{⬚}} \\ {4} & -{2} & {\placeholder{⬚}} \\ {-3} & {6} & {\placeholder{⬚}}\end{bmatrix}=\begin{bmatrix}{15} & {-3} & {\placeholder{⬚}} \\ {12} & -{6} & {\placeholder{⬚}} \\ {-9} & {18} & {\placeholder{⬚}}\end{bmatrix}`

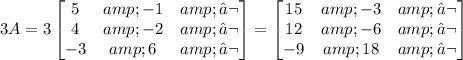
Now, we can subtract D:

`3A-D=\begin{bmatrix}{15} & {-3} & {\placeholder{⬚}} \\ {12} & -{6} & {\placeholder{⬚}} \\ {-9} & {18} & {\placeholder{⬚}}\end{bmatrix}-\begin{bmatrix}{-3} & {0} & {\placeholder{⬚}} \\ {4} & {7} & {\placeholder{⬚}} \\ {2} & {-1} & {\placeholder{⬚}}\end{bmatrix}`

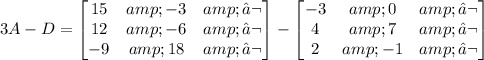
Then:

`\begin{gathered} 3A-D=\begin{bmatrix}{15-(-3)} & {-3-0} & {\placeholder{⬚}} \\ {12-4} & {-6-7} & {\placeholder{⬚}} \\ {-9-2} & {18-(-1)} & {\placeholder{⬚}}\end{bmatrix} \\ 3A-D=\begin{bmatrix}{18} & {-3} & {\placeholder{⬚}} \\ {8} & {-13} & {\placeholder{⬚}} \\ {11} & {19} & {\placeholder{⬚}}\end{bmatrix} \end{gathered}`

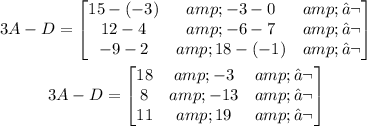
Finally, let us find D*C=

`D\ast C=\begin{bmatrix}{-3} & {0} & {\placeholder{⬚}} \\ {4} & {7} & {\placeholder{⬚}} \\ {2} & {-1} & {\placeholder{⬚}}\end{bmatrix}\ast\begin{bmatrix}{-3} & {0} & {2} \\ {4} & {1} & {-1} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

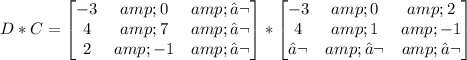
It is possible to multiply both matrices because the number of columns for D is equal to the number of rows for C.

Then:

Simplify the operations. Then:

`D\ast C=\begin{bmatrix}{9} & {0} & {-6} \\ 16 & {7} & {1} \\ {-10} & {-1} & {5}\end{bmatrix}`