Consider the formulae from Inverse Trigonometry,

Solve for the first angle as,
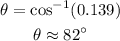
Thus, the required angle measure is 82 degrees approximately.
Solve for the second angle as,
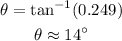
Thus, the required angle measure is 14 degrees approximately.
Solve for the third angle as,
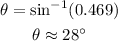
Thus, the required angle measure is 28degrees approximately.
Solve for the fourth angle as,
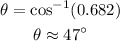
Thus, the required angle measure is 47 degrees approximately.
Solve for the fifth angle as,
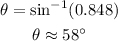
Thus, the required angle measure is 58 degrees approximately.