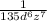Question

Exponential Rules Level 3

Answer 1

The expression to simplify is:

`((3d^3z)^(-3))/(5d^(-3)z^4)`

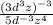
First, we will use the power rule of exponents to simplify the numerator. The rule is:

Simplifying, we have:

`\begin{gathered} ((3d^3z)^(-3))/(5d^(-3)z^4) \\ =((3)^(-3)(d^3)^(-3)z^(-3))/(5d^(-3)z^4) \\ =((1)/(27)d^(-9)z^(-3))/(5d^(-3)z^4) \end{gathered}`

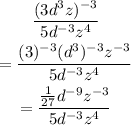
Now, we use another exponent rule shown below to simplify it further. The rule is:

So, we have:

`\begin{gathered} ((1)/(27)d^(-9)z^(-3))/(5d^(-3)z^4) \\ =\frac{(1)/(27)^{}}{5d^(-3+9)z^(4+3)} \\ =((1)/(27))/(5d^6z^7) \end{gathered}`

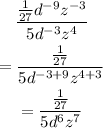
Now, we can just simplify the constants to get our final answer:

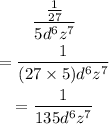
`\begin{gathered} ((1)/(27))/(5d^6z^7) \\ =(1)/((27*5)d^6z^7) \\ =(1)/(135d^6z^7) \end{gathered}`The final answer is:
`(1)/(135d^6z^7)`