Question

(a) Determine the intercepts. (b) Based on the graph, tell whether the graph is symmetric with respect to the x-axis, the y-axis, and/or the origin. (c) Based on the graph, tell whether the function is even, odd. or neither. (d) List the intervals on which ſ is increasing. List the intervals on which fis decreasing. (e) List the numbers, if any, at which f has a local maximum value. What are these local maxima values? (f) List the numbers, if any, at which f has a local minimum value. What are these local minima values?

Answer 1

Problem

Solution

Part a

For this case the x intercepts are:

(-5,0) , (-1,0) and (5,0)

The only y intercept is given by: (0,-3)

Part b

For this case we can see that f(x) =-f(x) for one of the side sof the graph so then we can conclude that the graph is symmetric repect to the x axis

Part c

For this case f(-x) =-f(x) so then we can conclude that the function is odd

Part d

Intervals increasing:

`(-\infty,-3)U(2,\infty)`

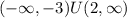
Intervals decreasing:

`(-3,2)`

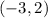
Part e

For this case the local maximum occurs at x=-3

(-3,5)

Part f

The local minimum for this case would be at x=2:

(2,-6)