Question

Given the exponential equation 4x = 64, what is the logarithmic form of the equation in base 10?

Answer 1

It is x = log 64 / log 4

Answer 2

`x=(log 64)/(log 4)`

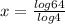
Explanation:

Given the exponential equation 4^x = 64

To convert exponential equation into log equation we use the rule

b^x = a then log_b(a)=x

the base of exponent becomes the base of log equation

4^x = 64 becoes

`log_4(64) = x`

WE need log with base 10, but we got log with base 4

USe change of base formula to get base 10

log_b(a)= log(a)/ log(b)

`(log 64)/(log 4) = x`

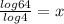
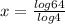`x=(log 64)/(log 4)` has log with base 10