Question

Evaluate a³-5g+(34-30)^0.5*(g+1)^0.5/2 if a=2 and g = 3

Answer 1

We are given the following expression

`a^(3)-5g+\sqrt[]{34-30}+\frac{\sqrt[]{g+1}}{2}`

whenever a=2 and g=3. What we should do, is replace the values of a and g and then operate accordingly. We will do this expression by expression and then operate eache term.

Consider the term a³. If a=2, then

`a^(3)=2^(3)=8`

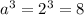
in the case for 5g, if g=3, then

`5\cdot g=5\cdot3=15`

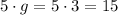
Now, let us analize sqrt(g+1), if g=3, then g+1=4. Then

`\frac{\sqrt[]{g+1}}{2}=\frac{\sqrt[]{4}}{2}`

in this case, we will always use positive square roots, so

`\frac{\sqrt[]{g+1}}{2}=\frac{\sqrt[]{4}}{2}=(2)/(2)=1`

Finally, we will calculate the remaining term

`\sqrt[]{34-30}=\sqrt[]{4}=2`

Then, the final procedure would be

`8-15+2+1\text{ = 11-15 =-4}`

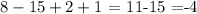
So the final answer is -4