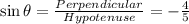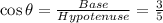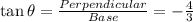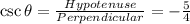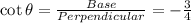Answer:
Here, we have
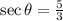
Since
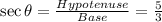
So, for the angle θ,
Hypotenuse = 5 and Base = 3
Using Pythogoras theorem,
(Hypotenuse)² = (Base²) + (Perpendicular )²
(5 )² = ( 3 )² + (Perpendicular )²
⇒ Perpendicular = 25 - 9 = √16 = 4
we have given θ lie in IV quadrant. In IV quadrant cos and sec are positive function but sine, cosec, tan and cot are negative.