The triangle MNO
M(-7,3)
N(9,8)
O(2,16)
Was dilated with respect of the origin resulting the triangle M'N'O'
M'(-10.5,4.5)
N'(13.5,12)
O'(3,24)
A dilation involves the multiplication of the coordinates of each vertex of the figure by a determned scale factor k.
P → P'
(x,y) (xk, yk)
So to determine the scale factor used you have to divide the coordinates of a dilated point by the coordinates of the corresponding original point, for example for M' and M, you have to compare the corresponding coordinates, that is
x-coordinate of M' and the x-coordinate of M
-or-
y-coordinate of M' and the y-coordinate of M
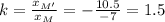
-or-
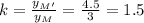
The scale factor is k=1.5
The algebraic description of the transformation is:
MNO(x,y)→M'N'O'(1.5x,1.5y)