Question

Two objects collide and stick together after the collision. One object moves with v before the collision and has 1/3 the mass of the other object which is initially stationary. What fraction of the original kinetic energy do the stuck pair carry?

Answer 1

Given:

The initial velocity of one of the objects is v.

The mass of that same object is 1/3 of the mass of the other object.

To find:

The fraction of the original kinetic energy that the stuck pair carry.

Step-by-step explanation:

Let us assume that the mass of the object that was initially stationary is m. Thus the mass of the other object is m/3

From the law of conservation of momentum,

`(m)/(3)v=((m)/(3)+m)u`

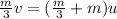
Where u is the velocity of the objects after the collision.

On simplifying the above equation,

`\begin{gathered} (m)/(3)v=(4m)/(3)u \\ \implies v=4u \\ \implies u=(v)/(4) \end{gathered}`

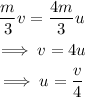
The total initial kinetic energy of the system is,

`\begin{gathered} KE_i=(1)/(2)*(m)/(3)v^2 \\ =(mv^2)/(6) \end{gathered}`

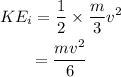
The kinetic energy of the stuck pair is,

`\begin{gathered} KE_f=(1)/(2)((m)/(3)+m)u^2 \\ =(1)/(2)*(4m)/(3)*(v^2)/(4^(^2)) \\ =(mv^2)/(24) \end{gathered}`

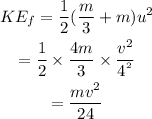
On taking the ratio of the final to initial kinetic energy of the system,

`\begin{gathered} (KE_f)/(KE_i)=((mv^2)/(24))/((mv^2)/(6)) \\ =(6)/(24) \\ =(1)/(4) \end{gathered}`

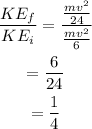
Final answer:

The stuck pair carry 1/4 th of the original kinetic energy.