Question

A point is chosen at random in the square shown below. Find the probability that the point is in the shaded circular region. Each side of the square is 6 cm, and the radius of the circle is 3 cm. Use the value 3.14 for pie. Round your answer to the nearest hundredth.

Answer 1

0.79

Explanation:

We have that if a point is chosen at random in the square, the probability that the point is in the shaded circular region is the ratio of the area of the circle to the area of the square.

We calculate the area in each case, just like this:

`\begin{gathered} A_s=l^2=6^2=36cm^2 \\ A_c=\pi\cdot r^2=3.14\cdot3^2=28.26cm^2 \end{gathered}`

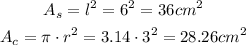
Knowing the areas, now we can calculate the probability:

`\begin{gathered} p=(28.26)/(36)=0.785\cong0.79 \\ p=0.79 \end{gathered}`

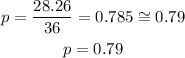
Therefore, the probability that the point chosen in a square is also in the circular region is 0.79