Question

One number is 7 more than another. The difference between their squares is 161. What are the numbers?

Answer 1

let's say the numbers are "a" and "b"

now, we know one of them is 7 more than the other, so hmmm let's say "b" is 7 more than "a", so b = a + 7

the difference of their squares is 161, alrite


`\bf a^2-b^2=161\qquad b=a+7\implies a^2-(a+7)^2=161 \\\\\\ a^2-(a^2+14a+49)=161\implies \underline{a^2-a^2}-14a-49=161 \\\\\\ -14a-49=161\implies -49-161=14a\implies -210=14a \\\\\\ \cfrac{-210}{14}=a`

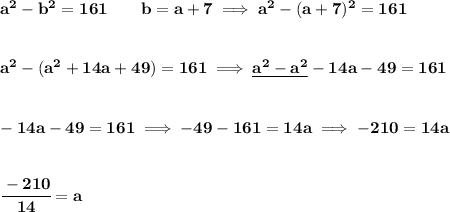
and surey you know how much that is

now, what's "b"? well, b = a + 7