Question

#13 solve a and b separately, note any restrictions to the derivative

Answer 1

Given:

`y=(x^2-a^2)/(x-a)`

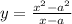
To find:

The derivative.

Step-by-step explanation:

a) Using the quotient rule,

`\begin{gathered} y^(\prime)=((x-a)(d)/(dx)(x^2-a^2)-(x^2-a^2)(d)/(dx)(x-a))/((x-a)^2) \\ =((x-a)(2x)-(x^2-a^2))/((x-a)^2) \\ =((x-a)(2x)-(x-a)(x+a))/((x-a)^2)\text{ \lbrack Since, }x^2-a^2=(x+a)(x-a)] \\ =((x-a)[2x-(x+a)])/((x-a)^2) \\ =((x-a)(x-a))/((x-a)^2) \\ y^(\prime)=1 \end{gathered}`

b)

By expanding the product and simplifying the quotient, we get

`\begin{gathered} y=(x^2-a^2)/(x-a) \\ =((x+a)(x-a))/((x-a)) \\ y=x+a \end{gathered}`

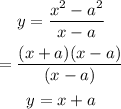
Differentiating with respect to x we get,

`y^(\prime)=1`

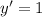
The part (a) answer and the part (b) answer are the same.

Hence verified.

Final answer:

The derivative for the given problem is 1.