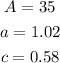Question

Solve for the remaining angle and sides of the triangle described below. Round to the nearest hundredth:B = 100, A = 45°, b = 3

Answer 1

The first step is to determine the value of the angle C, which we can determine by the fact that the sum of all the inner angles of any triangle is always 180°. From this, we are able to write the following:

`\begin{gathered} A+B+C=180\degree \\ 45\degree+100\degree+C=180\degree \\ C=180-100-45=35\degree \\ \\ C=35\degree \end{gathered}`

Now, to determine the values of a and c, we will use the Law of Sine, which brings the following relation:

`(\sin(A))/(a)=(\sin(B))/(b)=(sin(C))/(c)`

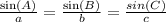
By substituting the values we already have, we can develop the following:

`\begin{gathered} (\sin(45\degree))/(a)=\frac{\sin (100\text{\degree)}}{3}=(\sin (35\degree))/(c) \\ \\ a=3(\sin(45\degree))/(\sin(100\degree))=3\cdot(1)/(0.985)=1.02 \\ c=3\cdot(\sin(35\degree))/(\sin(100\degree))=3\cdot(0.574)/(0.985)=0.58 \end{gathered}`

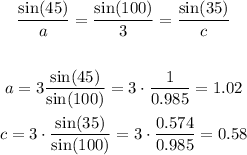
From the solution developed above, we are able to conclude that the solution of the present problem is:

`\begin{gathered} A=35\degree \\ a=1.02 \\ c=0.58 \end{gathered}`