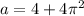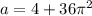This linear ODE has characteristic equation
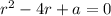
with roots
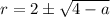
, which gives solutions of the form

There are three cases to consider:
(1) If
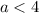
, then the solution will be exactly what we see above. However, the initial conditions force both

.
(2) If
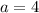
, we're left with
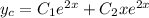
where
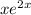
is added to the solution set to account for a second solution that is linearly independent of the first solution. Again, we get

.
(3) If
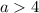
, then the square root introduces a factor of

that admits the solution
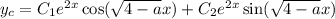
In this case, we arrive at
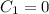
, and from the second condition we get
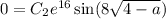
In order that

, we require that
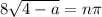
, where

is any integer. Solving for

, we get
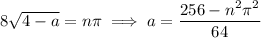
When
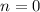
, we arrive at
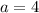
, but remember that we're assuming that
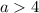
, so logically the three smallest values of

that are allowed occur for

. (
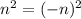
, so we can just look at positive integers

.)
Unfortunately, I'm not sure exactly what's going on next. Checking with a computer, the solution is supposed to be
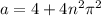
(Again, not sure why this is the case, but let's move on.) When

, we have the least values, which are, respectively,