Question

(PLEASE HELP)

If a tree diagram were drawn to determine the number of possible outcomes when choosing one of 2 shirts, one of 8 ties, and one of 4 jackets, how many leaves would there be
  A.

64
  B. 16  
C. 14  
D. 32

Answer 1

Option A is correct that is 64 leaves would be there.

Explanation:

Total Number of ties = 8

Total number of shirts = 2

Total number of jackets = 4

No of ties have to be chosen = 1

No of shirt have to be chosen = 1

No of jacket have to be chosen = 1

we use combination to find number of ways,

`^(n)\textrm{C}_(r)=(n!)/(r!\,(n-r)!)`

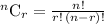
No way of choosing a tie =
`^(8)\textrm{C}_(1)=(8!)/(1!\,(8-1)!)=(8!)/(1!\,7!)=8`

No way of choosing a shirt =
`^(2)\textrm{C}_(1)=(2!)/(1!\,(2-1)!)=(2!)/(1!\,1!)=2`

No way of choosing a jacket =
`^(4)\textrm{C}_(1)=(4!)/(1!\,(4-1)!)=(4!)/(1!\,3!)=4`

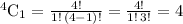
Total Number of ways of selection = 2 × 4 × 8 = 64

Therefore, Option A is correct that is 64 leaves would be there.

Answer 2

a)64 it 2*4*8=64 it is multiplied