Answer:
Option C - 2833 sq.m.
Explanation:
Given : A conical grain storage tank that has a height of 62 meters and a diameter of 24 meters.
To find : What is the surface area of a conical grain storage tank?
Solution :
The formula of surface area of a conical grain storage tank is
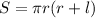
Where, r is the radius and l is the slant height.
Height of conical tank = 62 m
Diameter of conical tank = 24 m
Radius of conical tank = 12 m
The slant height is

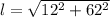
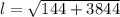
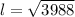
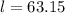
Substitute r and l in the formula,



Approximately,
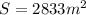
Therefore, Option C is correct.
The surface area of a conical grain storage tank is 2833 sq. m.