Question

Factorise fully ( − 3)(^2+ 4 − 11) + ( − 3)^2

Answer 1

Step 1

Given;

`(x-3)(x^2+4x-11)+(x-3)^2_{}`

Required; To factorize the problem

Step 2

Find the GCF

`\text{The GCF is x-3 because it is common}`

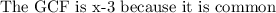
Hence, we will factorize thus and have;

`\text{GCF(}\frac{Total\text{ first term}}{\text{GCF}}+\frac{Total\text{ second term}}{\text{GCF}})`

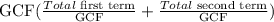
Applying this we will have;

`x-3(((x-3)(x^2+4x-11))/(x-3)+((x-3)^2)/(x-3))`

Therefore, we will now factorize (x²+5x-14) by finding the terms that when added together gives 5x and when multiplied together gives -14x²

`\begin{gathered} \text{These factors are 7x and -2x} \\ \end{gathered}`

Replace 5x with (7x-2x)

`x^2+7x-2x-14`

Grouping the four terms in twos, that is the first two as a pair and the remaining two as the other pair, we can bring out common terms from each pair. This is shown below:

`\begin{gathered} x^2\text{ }and\text{ }7x\Rightarrow x \\ -2x\text{ }and-14\Rightarrow-2 \end{gathered}`

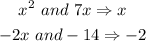
Therefore, using the factoring method shown in Step 2, we have the expression to be:

`\begin{gathered} x^2+7x-2x-14 \\ \text{Put the brackets} \\ (x^2+7x)(-2x-14) \\ \text{find the GCF in each bracket} \\ In\text{ the first bracket the GCF is x. In the second bracket the GCF is -}2 \\ x((x^2)/(x)+(7x)/(x))-2((-2x)/(-2)-(14)/(-2)) \\ \text{divide by GCF in each bracket} \\ x(x+7)-2(x+7) \end{gathered}`

Collecting the like terms, we, therefore, have the factorized expression to be:

`\Rightarrow(x+7)(x-2)`

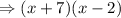
Therefore the full factorized expression will be;

`(x-3)(x+7)(x-2)`

The answer will therefore be ; (x-3)(x+7)(x-2)