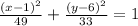Question

What is the equation of the ellipse in standard form?

Answer 1

Step-by-step explanation

The equation of an ellipse looks like this:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

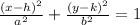
Where its center is located at (h,k), its vertices are located at (h+a,k) and (h-a,k) and its foci are located at (h+c,k) and (h-c,k) with c² = a² - b². Since we have the center, a vertex and a focus of the ellipse we can use them to find a, b, h and k.

We are told that the center of this ellipse is located at (1,6) which means that:

`(1,6)=(h,k)\rightarrow h=1\text{ and }k=6`

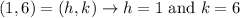
So for now we have:

`((x-1)^2)/(a^2)+((y-6)^2)/(b^2)=1`

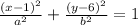
Now it's important to know that the focal length c is always a positive number. We know that one of the focus of the ellipse is located at (-3,6). Since the expression for the foci of the ellipse are (h+c,k) and (h-c,k) if we take (h,k)=(1,6) we obtain:

`\begin{gathered} (h+c,k)=(1+c,6) \\ (h-c,k)=(1-c,6) \end{gathered}`

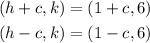
One of these two has to be equal to (-3,6). The correct one will be that with c>0. Then we get:

So as you can see the correct value of c is 4. Then we take the equation of c:

`\begin{gathered} c^2=a^2-b^2 \\ 16=a^2-b^2 \end{gathered}`

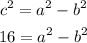
So we have an equation for a and b. We can use the coordinates of the vertex given by the question (8,6). We know that the vertices are located at (h+a,k) and (h-a,k). We can assume that a>0 without problems and we repeat the same calculations that we made for the focus and c but for the vertex (8,6) and a:

`\begin{gathered} \left(1+a,6\right)=(8,6)\Rightarrow1+a=8\Rightarrow a=8-1=7 \\ (1-a,6)=(8,6)\Rightarrow1-a=8\Rightarrow a=1-8=-7 \end{gathered}`

We take the first value because it's positive and we get a=7. Now that we have a we can find b using the equation of c:

`\begin{gathered} c^2=a^2-b^2\rightarrow4^2=7^2-b^2 \\ 16=49-b^2 \end{gathered}`

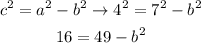
We add b² to both sides and we substract 16 from both sides:

`\begin{gathered} 16+b^2-16=49-b^2+b^2-16 \\ b^2=33\Rightarrow b=√(33) \end{gathered}`

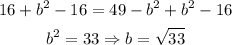
So we have found a, b, h and k which means that we can write the equation of the ellipse.

Answer

Then the answer is:

`((x-1)^2)/(49)+((y-6)^2)/(33)=1`