Answer:
The correct option is C.
Explanation:
Given information: Angles α and β are the two acute angles , β > ∝.
Given equation is
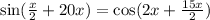
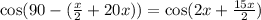
![[\because \sin (90-x)=\cos x]](https://img.qammunity.org/2018/formulas/mathematics/high-school/8cnxb0pokivd4exiya91eule4hx0q8m5e7.png)
Equating both the sides.
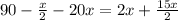
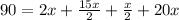

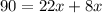

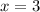
The value of angles is
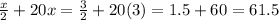
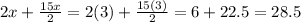
Since 61.5>28.5, therefore the value of β is 61.5. Option C is correct.