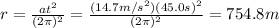Question

An acrobatic airplane performs a loop at an airshow. The centripetal acceleration the plane experiences is 14.7 m/s2.  If it takes the pilot 45.0 seconds to complete the loop, what is the radius of the loop? Round your answer to the nearest whole number.

Answer 1

The formula is 45^2(14.7)/4pi^2.
The answer is 754m.

Answer 2

754.8 m

Step-by-step explanation:

The centripetal acceleration is given by

`a=(v^2)/(r)`

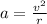
where v is the speed of the airplane and r is the radius of the loop.

We can rewrite the speed of the airplane as the ratio between the length of the circumference (
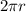`2 \pi r`) and the time taken:

`v=(2 \pi r)/(t)`

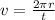
Substituting in the formula of the acceleration, we have

`a=((2 \pi)^2 r^2)/(t^2 r)=((2 \pi)^2 r)/(t^2)`

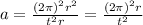
Re-arranging the formula and putting the numbers of the problem into it, we can find the radius of the loop, r:

`r=(at^2)/((2 \pi)^2)=((14.7 m/s^2)(45.0 s)^2)/((2 \pi)^2)=754.8 m`