Question

A software company sells an education version (e) and a commercial version (c) of its popular image editing software. During the month of January 500 copies of the software are sold with sales totaling $180,000. If the price of the education version is $150 and the price of the commercial version is $600 how many of each version were sold? Which system of equations matches the situation?

Answer 1

make 2 equations let x=150 y=600/180000  than plug and chug

Answer 2

A software company sells an education version and a commercial version of its popular image editing software. Let x be the number of education version copies sold and y be the number of commercial version copies sold.

1. During the month of January 500 copies of the software are sold, then

x+y=500.

2. If the price of the education version is $150, then x educational version copies cost $150x. If the price of the commercial version is $600, then y commercial version copies cost $600y. The total sales are $(150x+600y) that is $180,000, then

150x+600y=180,000.

3. The system that of equations matches the situation is

`\left\{\begin{array}{l}x+y=500\\150x+600y=180,000\end{array}\right..`

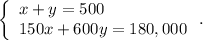
Solve this system. First, express x from the first equation:

x=500-y.

Substitute this x into the second equation:

150(500-y)+600y=180,000,

75,000-150y+600y=180,000,

450y=105,000,

`y=(105,000)/(450)=(700)/(3).`

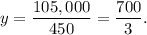
Then

`x=500-(700)/(3)=(800)/(3).`

Answer: they sold nearly 267 educational version copies and nearly 233 commercial version copies