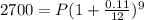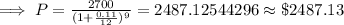Answer:
$ 2487.13 should be deposited. ( approx )
Explanation:
Since, future value formula,
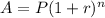
Where,
P = Principal amount,
r = rate per periods
n = number of periods,
Given,
A = $ 2,700,
t = 9 months,
Annual rate = 11%,
So, the monthly rate, r =
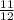 =
=
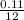
By substituting the values,