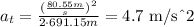Question

A car at the Indianapolis 500 accelerates uniformly from the pit area, going from rest to 290 km/h in a semicircular arc with a radius of 220 m.(a) Determine the tangential and radial acceleration of the car when it is halfway through the arc, assuming constant tangential acceleration.(b) If the curve were flat, what would the coefficient of static friction would be necessary between the tires and the road to provide this acceleration with no slipping or skidding?

Answer 1

(a)

In order to calculate the radial acceleration, use the following formula:

`a_r=(v^2)/(r)_{}`

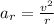
where:

v = 290 km/h

r = 220 m

write the speed in m/s:

290 km/h = 80.55 m/s

replace the values of v and r into the formula for ar:

`a_r=\frac{(80.55\text{ m/s)\textasciicircum{}2}}{220\text{ m}}=29.5\text{ m/s\textasciicircum{}2}`

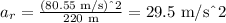
The tangential acceleration can be obtain by using the following formula:

`a_t=(v^2)/(2s)`

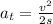
where s is the length of the arc traveled by the car.

s = 2πr/4 = 345.57 m

then, you have:

`a_t=(((80.55m)/(s))^2)/(2\cdot691.15m)=4.7\text{ m/s\textasciicircum{}2}`