Given data:
The mass of bowling ball is m=15 kg.
The height of ramp is h=5 m.
The velocity of bowling ball just before the collision can be calculated as,
![\begin{gathered} v=\sqrt[]{2gh}\ldots\ldots\text{.}\mathrm{}(1) \\ v=\sqrt[]{2*9.8*5} \\ v=9.9\text{ m/s} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/v68jl8zgm42b4h5sob7l.png)
Part (a)
The stationary mass is M=15 kg.
The velocity of bowling ball after collision will be,
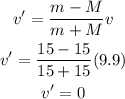
Since the velocity of bowling ball after the collision is zero, therefore the ball will not move back.
Part (b)
The stationary mass is M=30 kg.
The velocity of bowling ball after collision will be,
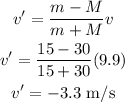
Here, negative sign indicates that the ball is movin in opposite direction after the collision.
The velocity after the elastic collision is 3.3 m/s. So, the height back up by the ball can be calculated by substitute the value of velocity in equation (1),
![\begin{gathered} v^(\prime)=\sqrt[]{2gh^(\prime)} \\ 3.3=\sqrt[]{2*9.8* h^(\prime)} \\ h^(\prime)=0.555\text{ m} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/ff6t88oj00jgd8ykynug.png)
Thus, the ball will returned to a height of 0.555 m.
Part (c)
The stationary mass is M=1000 kg.
The velocity of bowling ball after collision will be,

The velocity after the elastic collision is 9.6 m/s.
From equation (1),
![\begin{gathered} v^(\prime)=\sqrt[]{2gh^(\prime)} \\ 9.6=\sqrt[]{2*9.8* h^(\prime)} \\ h^(\prime)=4.7\text{ m} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/jjneibzo1esp8okf8j5i.png)
Thus, the ball will returned to a height of 4.7 m.