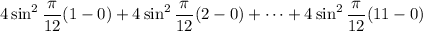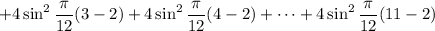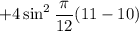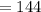Question

Let A_1, A_2, ..., A_12 be twelve equally spaced points on a circle with radius 1. Find (A_1 A_2)^2 + (A_1 A_3)^2 + ... + (A_11 A_12)^2. (The sum includes the square of the distance between any pair of points, so the sum includes 12choose2 = 66 terms.)

Answer 1

Let
`n` be a fixed positive integer. Then
`n` points can be equally spaced along the boundary of the unit disk in the complex plane, and their positions described in the complex plane are given by
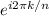
`e^(i2\pi k/n)`, where
`k=0,1,\ldots,n-1`.

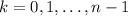
So, for any
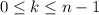
`0\le k\le n-1`, we can write


`A_k=e^(i2\pi k/n)=\cos\frac{2\pi k}n+i\sin\frac{2\pi k}n\equiv\left(\cos\frac{2\pi k}n,\sin\frac{2\pi k}n\right)`

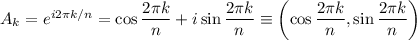
The distance between two points
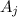
`A_j` and
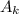
`A_k` is given by the norm of the difference of the points. We denote this by


`A_jA_k:=|A_j-A_k|`

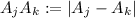
We're interested in all the possible distinct pairings, which means
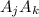
`A_jA_k` and
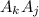
`A_kA_j` are to be considered the same, so to accomplish this we assume
`0\le j<k\le n-1`.

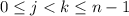
Then the sum we're interested in finding is


`\displaystyle\sum_(0\le j<k\le n-1)(A_jA_k)^2=(A_0A_1)^2+\cdots+(A_0A_(n-1))^2+(A_1A_2)^2+\cdots+(A_1A_(n-1))^2+(A_2A_3)^2+\cdots+(A_(n-2)A_(n-1))^2`

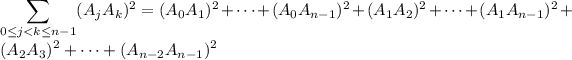
where this sum is identical to the one in your original question, except the indices of each point are shifted down by one.

We have


`(A_jA_k)^2=|A_j-A_k|^2`

`=\left|\left(\cos\frac{2\pi j}n,\sin\frac{2\pi j}n\right)-\left(\cos\frac{2\pi k}n,\sin\frac{2\pi k}n\right)\right|^2`

`=\left(\cos\frac{2\pi j}n-\cos\frac{2\pi k}n\right)^2+\left(\sin\frac{2\pi j}n-\sin\frac{2\pi k}n\right)^2`

`=\cos^2\frac{2\pi j}n-2\cos\frac{2\pi j}n\cos\frac{2\pi k}n+\cos^2\frac{2\pi k}n+\sin^2\frac{2\pi j}n-2\sin\frac{2\pi j}n\sin\frac{2\pi k}n+\sin^2\frac{2\pi k}n`

`=2-2\cos\frac{2\pi}n(j-k)`

`=4\sin^2\frac\pi n(j-k)`

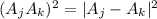
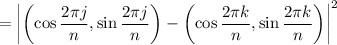
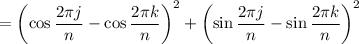
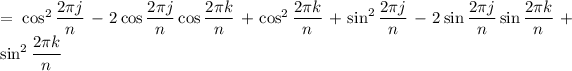
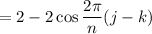
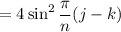
So we can express the sum as


`\displaystyle\sum_(0\le j<k\le n-1)4\sin^2\frac\pi n(j-k)=\sum_(0\le j<k\le n-1)4\sin^2\frac\pi n(k-j)=\sum_(k=1)^(n-1)\sum_(j=0)^(k-1)4\sin^2\frac\pi n(k-j)`

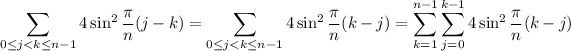
For example, if we take
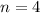
`n=4` points, we can see the points make up the vertices of a square with inradius 1, which means the distance between adjacent points (
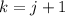
`k=j+1`) is
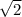
`\sqrt2`, while the distance between opposite points (
`k=j+2`, which gets counted only once) is
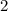
`2`. So we would expect the sum to be


`(A_0A_1)^2+(A_0A_2)^2+(A_0A_3)^2+(A_1A_2)^2+(A_1A_3)^2+(A_2A_3)^2=4(\sqrt2)^2+2(2)^2=16`

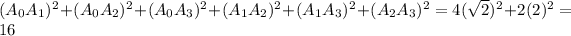
In terms of our sum, we would add


`\displaystyle\sum_(0\le j<k\le3)4\sin^2\frac\pi4(k-j)`

`=4\left(4\sin^2\frac\pi4\right)+2\left(4\sin^2\frac{2\pi}4\right)`

`=4(\text{distance between adjacent vertices})+2(\text{distance between opposite vertices})`

`=16`

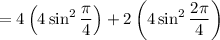
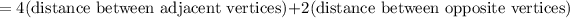
as required.

This was just an example to convince you that the formula works.

For
`n=12`, you would end up with


`4\sin^2\frac\pi{12}(1-0)+4\sin^2\frac\pi{12}(2-0)+\cdots+4\sin^2\frac\pi{12}(11-0)`

`+4\sin^2\frac\pi{12}(2-1)+4\sin^2\frac\pi{12}(3-1)+\cdots+4\sin^2\frac\pi{12}(11-1)`

`+4\sin^2\frac\pi{12}(3-2)+4\sin^2\frac\pi{12}(4-2)+\cdots+4\sin^2\frac\pi{12}(11-2)`

`+\cdots`

`+4\sin^2\frac\pi{12}(11-10)`

`=144`