Question

Given, what does this tell us about the relationship between the two functions?

Answer 1

one function is the inverse of the other

`\begin{gathered} f(x)=g^(-1)(x) \\ g(x)=f^-(x) \end{gathered}`

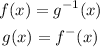
Step-by-step explanation

`\begin{gathered} f(x)=(x)/(2+x) \\ g(x)=(2x)/(1-x) \end{gathered}`

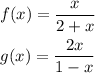
Step 1

Function Composition is applying one function to the results of another. · (g º f)(x) = g(f(x)), first apply f(), then apply g()

so

`\begin{gathered} f(g(x))=(((2x)/(1-x)))/(2+((2x)/(1-x))) \\ \text{evaluate} \\ f(g(x))=(((2x)/(1-x)))/((2-2x+2x)/(1-x))=(((2x)/(1-x)))/((2)/(1-x))=(2x(1-x))/(2(1-x))=x \\ f(g(x))=x \end{gathered}`

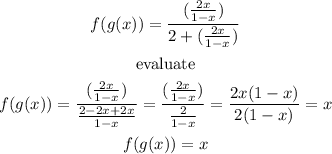
and

Step 2

g(f(x))

`\begin{gathered} g(x)=(2x)/(1-x) \\ g(f(x))=(2((x)/(2+x)))/(1-((x)/(2+x))) \\ g(f(x))=(2((x)/(2+x)))/(1-((x)/(2+x)))=((2x)/(2+x))/((2+x-x)/(2+x))=(2x(2+x))/(2(2+x))=x \\ g(f(x))=x \end{gathered}`

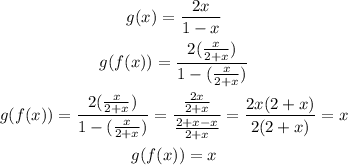
n mathematics, an inverse is a function that serves to “undo” another function. That is, if f(x) produces y, then putting y into the inverse of f produces the output x,

so the realtion between the functios is

one function is the inverse of the other

g is the inverse of f

f is the inverse of g

`\begin{gathered} f(x)=g^(-1)(x) \\ g(x)=f^-(x) \end{gathered}`

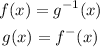
I hope this helps you