Question

Solve and graph each solution set.2 sf(x) 20, where f(x) = 3x - 1

Answer 1

Given the following inequality:

`2\leq f(x)\leq20`

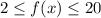
You know that:

`f\mleft(x\mright)=3x-1`

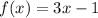
Then, you need to rewrite the inequality as follows:

`2\leq3x-1\leq20`

To solve the inequality, you can follow these steps:

1. Add 1 to all the three parts of the inequality:

`\begin{gathered} 2+(1)\leq3x-1+(1)\leq20+(1) \\ 3\leq3x\leq21 \end{gathered}`

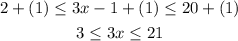
2. divide all the three parts of the inequality by 3:

`\begin{gathered} (3)/(3)\leq(3x)/(3)\leq(21)/(3) \\ \\ 1\leq x\leq7 \end{gathered}`

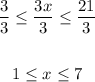
Notice that it can be expressed as a double inequality. This indicates that two inequalities are joined.

Then, to graph the solution on the Number Line, you need to follow the steps shown below:

1. Since both symbols are:

`\leq`

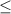
You can draw to draw a square bracket "[" on the number 1 and another square bracket "]" on the number 7.

2. Draw a line that connects or join the brackets.

Then, you get this graph:

Therefore, the answers are:

- Solution:

`1\leq x\leq7`

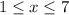
- Graph: Option A.